Invited Speaker----Dr. Reuven Segev

Dr. Reuven Segev, Professor, Ben-Gurion University, Israel
Reuven Segev is the H. Greenhill Chair Professor of Theoretical and Applied Mechanics at the Department of Mechanical Engineering at Ben-Gurion University of the Negev, Beer-Sheva, Israel. His research is concerned with the applications of geometrical and analytical methods to the mechanics of continuous medium.
Professor Segev received his B.Sc. (1976) and M.Sc. (1978) in mechanical engineering at Ben-Gurion University. He completed his Ph.D. in 1981 at the University of Calgary, Canada. Since 1981, he has been affiliated with Ben-Gurion University. During the period of 2003-2008, he served as the Head of the department and in the period 2014-2017 he served as the Associate Dean of the Faculty of Engineering Science at Ben-Gurion University.
Professor Segev spent sabbatical years with C. Truesdell at Johns Hopkins U. in 1987/88, with M. Epstein at the U. of Calgary in 1995/96, and with J. Goddard, U. of California, San Diego 2008/09.
Speech Title: Worst-case loadings and load capacity ratios of structures
Aims: Engineering stress analysis for a given structure is usually carried out for some assumed loading conditions and using experience in order to study worst case situations. We present a procedure that, for an elastic perfectly plastic structure, will enable the designer to make sure that the structure can sustain loads the maxima of which is no higher than some given value, no matter how they are distributed.
Methods: Notions from functional analysis are used in order to prove the results outlined below and construct algorithms for the evaluation of worst-case loadings. All are based only on the geometry of the structure.
Results: For an elastic perfectly-plastic structure, for which the yield stress is
σY , there is a number,
C, the load capacity ratio, that depends only on the geometry of the structure, such that the structure will not collapse plastically for any loading, the maximal magnitude of which over whole body is t
max as long as t
max≤σ
YC . The load capacity ratio is given by
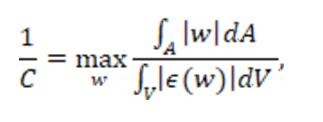
where the maximum is taken over all vector fields
W over the structure, and
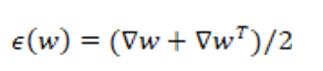
.
Algorithms for the computation of
C and worst-case loadings have been proposed and some examples will be presented.
Conclusions: The foregoing results may assist a designer in reducing the inherent uncertainty in the stress analysis process.


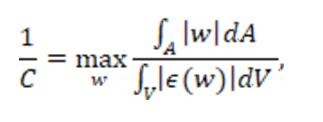
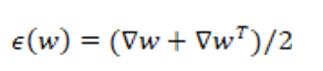 .
Algorithms for the computation of C and worst-case loadings have been proposed and some examples will be presented.
.
Algorithms for the computation of C and worst-case loadings have been proposed and some examples will be presented.